17. Summary
Summary
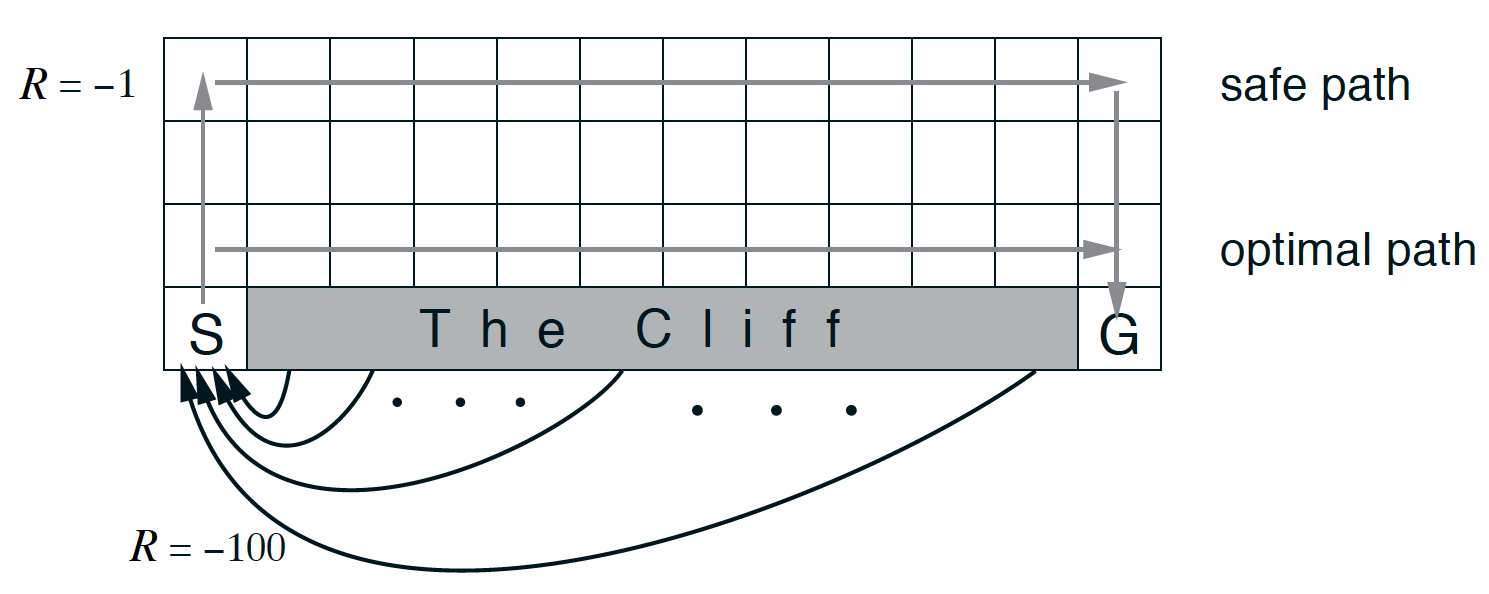
The cliff-walking task (Sutton and Barto, 2017)
## TD Prediction: TD(0)
- Whereas Monte Carlo (MC) prediction methods must wait until the end of an episode to update the value function estimate, temporal-difference (TD) methods update the value function after every time step.
- For any fixed policy, one-step TD (or TD(0)) is guaranteed to converge to the true state-value function, as long as the step-size parameter \alpha is sufficiently small.
- In practice, TD prediction converges faster than MC prediction.

## TD Prediction: Action Values
- (In this concept, we discussed a TD prediction algorithm for estimating action values. Similar to TD(0), this algorithm is guaranteed to converge to the true action-value function, as long as the step-size parameter \alpha is sufficiently small.)
## TD Control: Sarsa(0)
- Sarsa(0) (or Sarsa) is an on-policy TD control method. It is guaranteed to converge to the optimal action-value function q_*, as long as the step-size parameter \alpha is sufficiently small and \epsilon is chosen to satisfy the Greedy in the Limit with Infinite Exploration (GLIE) conditions.

## TD Control: Sarsamax
- Sarsamax (or Q-Learning) is an off-policy TD control method. It is guaranteed to converge to the optimal action value function q_*, under the same conditions that guarantee convergence of the Sarsa control algorithm.

## TD Control: Expected Sarsa
- Expected Sarsa is an on-policy TD control method. It is guaranteed to converge to the optimal action value function q_*, under the same conditions that guarantee convergence of Sarsa and Sarsamax.

## Analyzing Performance
- On-policy TD control methods (like Expected Sarsa and Sarsa) have better online performance than off-policy TD control methods (like Q-learning).
- Expected Sarsa generally achieves better performance than Sarsa.